In the information part, the rectangular waveguides are explained in detail. TM and TE modes are investigated separately (but in parallel) and the formulas for cut-off wave-number (kc), propagation constant (b ), cut-off wavelength (l c), guide wavelength (l g), phase velocity (up), attenuation constant due to dielectric loss (a d) and wave impedance (Z) are derived for both modes. So, given the dimensions of the rectangular waveguide (a,b), the properties of the filling material (m ,e ), the operating frequency (f) and the mode of the rectangular waveguide (TMmn or TEmn), we can calculate any of the outputs mentioned above. In the design and analysis part, the program calculates all the outputs given the inputs. The user enters the dimensions of the rectangular waveguide (a,b), the properties of the filling material (m ,e ), the operating frequency (f) and the mode of the rectangular waveguide (TMmn or TEmn) and the program calculates the cut-off wave-number (kc), the propagation constant (b ), the cut-off wavelength (l c), the guide wavelength (l g), the phase velocity (up), the attenuation constant due to dielectric loss (a d) and the wave impedance (Z). one can also see the graph of cut-off frequency versus the dimensions of the waveguide. Furthermore, the user can design a rectangular waveguide using the program. If the user enters the properties of the medium and the frequency, with which he/she wants his/her rectangular waveguide to travel, the program designs a rectangular waveguide with the dimensions so that the given frequency is inserted in the middle of TE10 and TE20 modes. For the design, we always take a as being equal to 2b. in this case, the lowest two cut-off frequencies are for TE10 and TE20 modes. From the formulas of the information part, we get
Using a=2b and f={(fC-TE)10+(fC-TE)20} / 2; the program calculates a and b. In other words, it designs a rectangular waveguide for the given material properties and operating with the given frequency. If you encounter any problems, you can send autors e-mail: | |
| |
Rectangular Waveguides
and 
Subscribe to:
Post Comments (Atom)
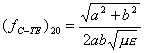
This is my first time i visit here. I found so many entertaining stuff in your blog, especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the enjoyment here! Keep up the good work.
ReplyDeleteThank you. Happy to know that you are enjoying my blog! I'll make posts better !!! I'm thinking about new site with more information and discussion board.
Delete