Generally branch-line couplers are 3dB, four ports directional couplers having a 90° phase difference between its two output ports named through and coupled arms. Branch-line couplers (also named as Quadrature Hybrid) are often made in microstrip or stripline form.
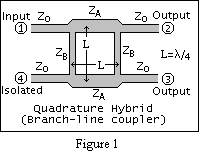
The geometry of the branch-line coupler is shown in Figure1. A branch-line coupler is made by two main transmission lines shunt-connected by two secondary (branch lines). As it can be seen from the figure, it has a symmetrical four port. First port is named as Input port, second and third ports are Output ports and the fourth port is the Isolated port. The second port is also named as direct or through port and the third port is named as coupled port. It is obvious that due to the symmetry of the coupler any of these ports can be used as the input port but at that time the output ports and isolated port changes accordingly. When we analysis the scattering matrix of this coupler we will see also the result of that symmetry in scattering matrix. Considering the dimensions of the coupler the length of the branch line and series line is generally chosen as the one fourth of the design wavelength . As it is shown in Figure 1, if we name the length of series and stub transmission lines as L then L can be find as following:
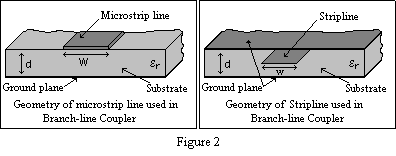
At that point we will se the calculation of the other dimension parameter of transmission lines; w/d ratio. We generally design branch-line couplers in two forms: Microstrip line and Stripline. Geometry of the microstrip line and stripline can be seen from Figure2. According to the impedance choice of the series and stub microstrip transmission lines we can calculate the w/d ratios of the those lines in microstrip form by using the following formulas: Given er and Z0
Considering the Stripline branch-line coupler design, we can calculate w/d ratios for each (stub and series) transmission line in the branch-line coupler with following calculations:
2.ANALYSIS OF BRANCH-LINE COUPLER 2.1.Even-odd mode analysis and S-parameters
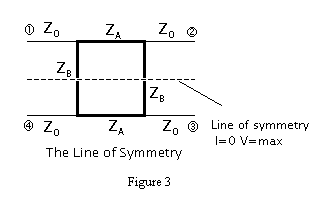
In the analysis of the branch-line coupler we consider the scattering matrix of the coupler. In order to find them we use even-odd .mode analysis. In both mode we divide the branch-line coupler symmetrically as in the Figure 3.
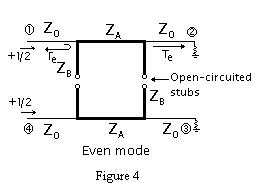
Generally considering that we give V voltage to the Input port. In the even odd mode analysis we consider it we give that V voltage in even mode ½ of it to Input port and rest to the Isolated port and for the odd mode we give Input port ½ of it and to the isolated port �1/2 of it. Furthermore, while making even-odd mode analysis, for the even mode we think that the stubs of the divided circuit are open circuited and for the odd mode they are short circuited. For this analysis, if we consider the superposition of the incoming voltage, it results as V voltage to the Input and 0 voltage to the Isolated port. Furthermore we have for each mode incident and reflected waves, for even mode it is illustrated in the Figure 4. As it is seen we have an incident wave ½ of the actual voltage and at first stub we have a reflection having a reflection coefficient Ge and at second port a transmitted signal having transmission coefficient Te. Considering the contribution of the even mode to the port waves for first port we have 1/2VGe, for second port we have 1/2VTe, for third port 1/2VTe, and for the fourth port 1/2VGe.
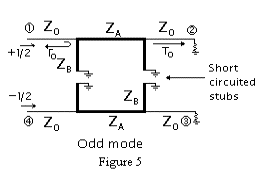
In addition, for odd mode incident and reflected waves are illustrated in the Figure 5. As it is seen we have an incident wave ½ of the actual voltage at first port and �1/2 of it at fourth port as incoming wave. Also at first stub we have a reflection having a reflection coefficient Go and at second port a transmitted signal having transmission coefficient To. Considering the contribution of the odd mode to the port waves for first port we have 1/2VGo, for second port we have 1/2VTo, for third port -1/2VTo, and for the fourth port --1/2VGo. At this point, we express the emerging wave at each port of the branch-line coupler as the superposition of the even and odd mode waves as following:
B1=(1/2Ge+1/2Go)V 1.7 B2=(1/2Te+1/2To)V 1.8 B3=(1/2Te-1/2To)V 1.9 B4=(1/2Ge-1/2Go)V 1.10 The ABCD matrix is used to find the overall transmission and reflection characteristics of the network. Having YA=1/ZA and YB=1/ZB we have the ABCD matrix of even and odd mode. For even mode ABCD parameters are as following: Since we have l=l/4 (and work with our design frequency), bl=(2p/l)*(l/4)=p/2 Therefore cosbl=0 and sinbl=1 and the ABCD matrix is following:
For the odd mode ABCD matrix: Since we have l=l/4 and so bl=(2p/l)*(l/4)=p/2 So cosbl=0 and sinbl=1 and the ABCD matrix is following At that point we can find Ge, Go, Te, To by using following equations: Then solving above equations with parameters of even and odd mode ABCD matrixes at center frequency where ¦=np/l=np/4l :
At this time we can say that B1/V=S11, B2/V=S12, B3/V =S13 and B4/V =S14. Therefore S-Parameters are as following:
And the scattering matrix of Branch-line coupler is 2.2. Matching Condition Looking above equations if we consider the matching condition;
then S11 and S14 becomes zero. In that matching case; the power entering port1is evenly divided between ports 2 and 3 with a 90° phase shift between these output ports. No power is coupled to port 4 (isolated port). Therefore, the isolation and directivity of that matched coupler, which will be mentioned in following part, is very high (for perfect case infinity), at center frequency.
|
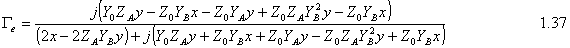 |
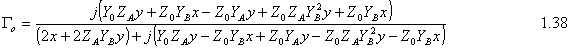 |
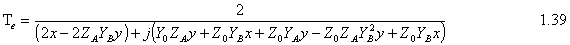 |
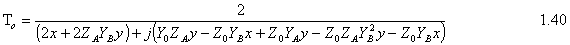 |
At this point, if we use (1.25), (1.26), (1.27), (1.28), then we get all the necessary s-parameters in our hand. After finding s-parameters, we can find magnitude of s-parameters and plot the magnitude verses frequency plot. This simulation program can plot the magnitude of s-parameters vs. frequency plot.
References:
1. Fooks, E. H. Microwave engineering using microstrip circuits, Prentice Hall New York 1990
2. Pozar, David M. Microwave Engineering Second Edition, Wiley, New York 1998
Prof. M. Irsadi Aksun,
Electrical and Electronics Engineering Dept.
Bilkent University, Ankara, Turkey
Email: irsadi@ee.bilkent.edu.tr
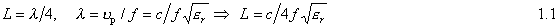
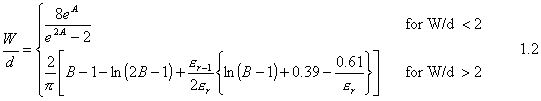
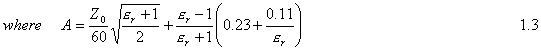

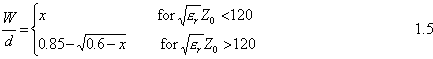


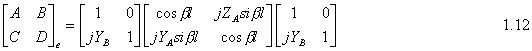
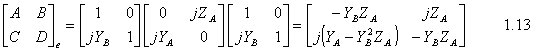

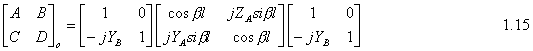
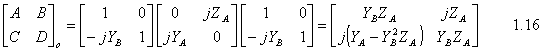




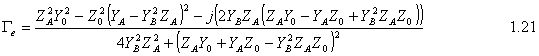
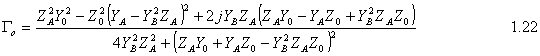
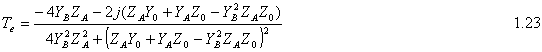
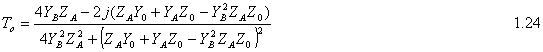




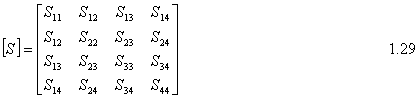

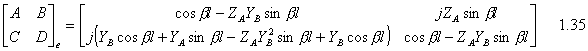
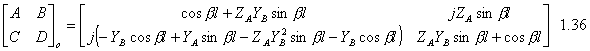
No comments:
Post a Comment